සිංහලෙන් ML Algorithms: Linear Regression

 

 

හැදින්වීම 

Machine Learning (ML) ඇල්ගොරිතම පිළිබඳ ලිපි මාලාවේ පළමු ලිපිය මෙය වනු ඇත. මෙම ලිපි මාලාවේ අපි සාකච්ඡා කරනු ලබන සිද්ධාන්ත සදහා Python පරිගණක භාෂාවෙන් උදාහරණයන් ඔබට මෙම සබැඳියෙන් ලබා ගත හැකිය.

Linear Regression (ලීනියර් රිග්රේෂන්) යනු ඕනෑම ML නවකයෙකු ML ඇල්ගොරිතම අධ්‍යයනය කිරීමේදී ඉගෙන ගන්නා පළමු ML ඇල්ගොරිතමයයි. මෙය සිංහලෙන් Machine Learning යන අපගේ පෙර ලිපියේ සඳහන් කළ පරිදි අධීක්ෂණය යටතේ ඉගෙනුම සිදු කරන (Supervised Learning) ඇල්ගොරිතමයකි. එය සන්තතික පරිමාණයක අගයන් පුරෝකථනය කිරීමට භාවිත කරයි. එනම් පෙර ලිපියේ සදහන් කල වර්ගීකරණ ගැටළු නොව අනෙත් වර්ගයේ ගැටලුයි මේ ක්‍රමයෙන් විසදිය හැක්කේ.

වෙනත් වචන වලින් කිවහොත්, අපට ආදාන (input) නැතහොත් ස්වායක්ත විචල්‍යයන් (පෙර ලිපියේ සාකච්ඡා කළ පරිදි Features) කිහිපයක් සහ ප්‍රතිදානය නැතිනම් පාරයක්ත විචල්‍යයක් අතර රේඛීය සම්බන්ධතාවයක් සොයා ගැනීමට මෙම ක්‍රමය භාවිත කළ හැකිය. එම සම්බන්ධතාවය පහත ආකාරයෙන් පෙන්විය හැක.

සමීකරණය 1: Linear Regression සමීකරණය

මෙහි, 

• X1, X2, ... , Xm ආදාන (input) නැතහොත් ස්වායක්ත විචල්‍යයන් ය 
• Y යනු  ප්‍රතිදානය (output) නැතිනම් පාරයක්ත විචල්‍යයයි
• b යනු bias (බයස්) නැතිනම් අන්තක්කන්ඩය යි. 
• W1, W2, ... ,Wm යනු භාරයන් (weights) නැතහොත් සංගුණක පදයි.

එක් ආදානයක් (input) සමග මෙම සම්බන්ධතාව ඔබට වඩාත් හුරුපුරුදු විය හැකිය. එවැනි අවස්ථාවකදී මෙම සම්බන්ධතාවය පහත පරිදි වේ.

සමීකරණය 2: Simple Linear Regression සමීකරණය

මෙය අන් කිසිවක් නොව දිවිමාන සරල රේඛාවක සමීකරණය යි. මුල් සම්බන්ධතාව (සමීකරණය 1) නම් බහුමාන සරල රේඛාවක සමිකරණයයි.

Linear Regression ගැටළු වලදී, අප කරන්නේ අප සතුව ඇති දත්ත භාවිත කර (අපගේ පෙර ලිපියේ සාකච්ඡා කළ පරිදි Features සහ ලේබල් භාවිත කර) භාර (weights) පදවල (එනම් W1, W2, ..., Wn) සහ bias  පදයේ (එනම් b) අගයන් නිර්ණය කිරීමයි. මෙය ගණිතයේ එන Linear Regression ම වන අතර ගැටලුව විසදීමේ ක්‍රමවේදය තරමක් දුරට වෙනස් විය හැකිය.

ගණිතමය පසුබිම

Simple Linear Regression

පළමුව මම එක් ආදානයක් (input) හා සම්බන්ධ ගණිතමය පසුබිම සලකා බලමු. බහු විචල්‍ය අවස්ථාව මෙහිම දිගුවකි.

ආදානය (input) නැතිනම් Feature එක (x) සහ ප්‍රතිදානය  (output)අතර සම්බන්ධය පහත පරිදි යැයි සිතමු.

සමීකරණය 3: Simple Linear Regression සමීකරණය

මෙහි m යනු භාර පදය වන අතර b යනු bias පදයයි.

අප සතු දත්ත කට්ටලයේ දත්ත ලක්ෂ්‍ය (Xi, Yi) ලෙස දී ඇතැයි ගනිමු. (එනම් {(X1, Y1), (X2, Y2), ..., (XN, YN)} ලෙස). දත්ත ලක්ෂ්‍ය N ගණනක් ඇතැයි ගනිමු. අපගේ අරමුණ වන්නේ y=mx+b යන සම්බන්ධතාව තෘප්ත කරන m සහ b අගයන් එම දත්තවලින් සොයා ගැනීමයි.  

පහත රූපයේ පරිදි නිල පාටින් සලකුණු කොට ඇත්තේ අපේ දත්ත ලක්ෂ්‍ය යි. කළු පාට රේඛාව තමයි අප විසින් සොයා ගත යුතු අවසාන විසදුම. එනම් අපගේ y=mx+b සම්බන්ධතාවය.

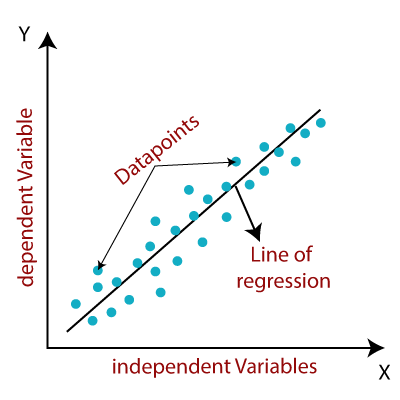රූපය 1: Simple Linear Regression ප්‍රස්ථාරික නිරූපනයක් 

පියවර 1: විචල්‍ය සදහා ආරම්භක අගයන් තොරා ගැනීම

ආරම්භයේදී m සහ b සදහා අභිමත අගයක් (ඔබ කැමති අගයක්) තෝරා ගන්න. දැන් අපට සරල රේඛාව සඳහා සමීකරණයක් ඇත. එනම්,

සමීකරණය 4: Simple Linear Regression සමීකරණය

පියවර  2: අතරමැදි ප්‍රතිදානය (output) ගණනය කිරීම

අපගේ දත්තවල Xi අගයන් (දත්ත කට්ටලයේ එනම් {(X1, Y1), (X2, Y2), ..., (XN, YN)} හි X1, X2, ... යන අගයන්) ඉහත සමීකරණයට ආදේශ කර එහි අගයන් ලබා ගන්න (එනම් f (Xi) = mXi + b අගයන්). මෙම f(Xi) අගයන් හි දෝෂය එනම්, Xi ප්‍රදානය කල විට සැබෑවටම පැමිණිය යුතු අගය වන Yi සහ අපට ලැබුණු පිළිතුර වන f(Xi) අතර  වෙනස පහත පරිදි සෙවිය හැකිය.

සම්බන්ධය 1: Simple Linear Regression දෝෂ ප්‍රකාශනය

පියවර 3: පිරිවැය ශ්‍රිතය (Cost Function) අර්ථ දැක්වීම

අපේ අවසාන අරමුණ වන්නේ අප දත්තවලට වඩාත්ම ගැළපෙන සරල රේඛාවේ m සහ b අගයන් සොයා ගැනීමයි. එහිදී අප සිදු කරන්නේ අපගේ පිළිතුරේ දෝෂය අවම වන පරිදි m සහ c හි අගයන් කිසියම් කාර්යක්ෂම ක්‍රමයකට වෙනස් කරමින් බැලීමයි.එහිදී අප ගැටලුවට ඔබින දෝෂ ප්‍රකාශනයක් නැතිනම් පිරිවැය ශ්‍රිතයක් (Cost Function) තෝරා ගත යුතුය. මෙහිදී අප Yi සහ f(Xi) අතර වෙනසෙහි වර්ග මධ්‍යන්‍ය අගය (එනම් (Yi - f(Xi) අගයන්හි හෙවත් දෝෂයේ වර්ගයන්හි  මධ්‍යන්‍ය අගය) පිරිවැය ශ්‍රිතය (Cost Function) ලෙස තෝරා ගනිමු. අපි මෙම පිරිවැය ශ්‍රිතය (Cost Function) අවමවන පරිදි m සහ c අගයන් තෝරා ගැනීමයි සිදු කළ යුත්තේ.

සමීකරණය 5: Simple Linear Regression වර්ගයන්හි  මධ්‍යන්‍ය දෝෂය 

මෙහි, 

• N යනු මුළු දත්ත ලක්ෂ්‍ය ගණනයි .
• 1N∑ni=1 යනු මධ්‍යන්‍යය යි 
• yi යනු සැබෑවටම පැමිණිය යුතු අගය 
• mxi + b යනු වත්මන් m සහ b අගයන්ට ලැබුණු ප්‍රතිඵලයයි.

සමීකරණය 6: Simple Linear Regression පිරිවැය ශ්‍රිතය

පියවර 4: m සහ b ට සාපේක්ෂව පිරිවැය ශ්‍රිතයෙහි (Cost Function) අවකලන සංගුණක සෙවීම

දෝෂය අවම වන දිශාවට m සහ b අගයන් විචලනය කිරීමට අපට පිරිවැය ශ්‍රිතයෙහි (Cost Function - f(m, b)) ආංශික අවකලන සංගුණක සෙවීම කළ යුතුය. එම ප්‍රකාශන පහත පරිදි වේ. 

සමීකරණය 7: Simple Linear Regression අවකල සංගුණක සෙවීම

සටහන : Gradient Descent ඇල්ගොරිතමය

Gradient descent (ග්‍රේඩියෙන්ට් ඩෙසෙන්ට්) යනු ප්‍රශස්තිකරණ (optimization - එනම් ශ්‍රිතයක උපරිම හෝ අවම අගයන් සෙවිම) ඇල්ගොරිතමයක්/ ක්‍රමයක් වන අතර, එය යම් ශ්‍රිතයක වැඩිම බැවුම ඔස්සේ ගමන් කරමින් ශ්‍රිතයක අවම අගයසෙවීමේ ක්‍රමයකි. මම ඇල්ගොරිතමය ක්‍රියා කරන ආකාරය මේ ලෙස පැහැදිලි කල හැක. අපි කදු බෑවුම් ප්‍රදේශයක, කදු මුදුනකට ගොස් බෑවුම් ස්ථානයක බෝලයක් තැබුවිට එය බෑවුම් ඔස්සේ ගමන් කර අවසානයේ නිම්නයක/ පහළම ස්ථානයක නතර වේ. මෙම අල්ගොරිතමයද ශ්‍රිතයක වැඩිම බෑවුම් ඔස්සේ (අවකල සංගුණකහි සෘණ දිශාව ඔස්සේ) ශ්‍රිතයෙහි  අවමය වෙත ළගා වීම සිදු කරයි. 

පහත රූපය බලන්න. එය අප පිරිවැය ශ්‍රිතයයේ (Cost Function) ප්‍රස්ථාරය යයි සිතන්න. තද නිල් පැහැයෙන් ඇත්තේ එහි අවම අගයන් ලැබෙන ප්‍රදේශ යි. කළුපාට ඊතලවලින් දක්වා ඇත්තේ වැඩිම බැවුම් දිශාවන් ය. අපි අභිමත  m සහ b අගයන්ගෙන් ආරම්භ කල විට  ආරම්භයෙදී අපේ පිරිවැය ශ්‍රිතයයේ අගය ඕනෑම අගයක් විය හැකිය. එනම් ආරම්භයේදී අපි මෙමෙ බැවුම් ප්‍රදේශයේ (පහත රුපයේ) ඕනෑම ස්ථානයක් සිටිය හැකිය. එම ස්ථානයේ සිට මෙම ඊ හිස්වලින් දක්වන දිශාවන් ඔස්සේ ගමන් කල විට නිරායාසයෙන්ම අපි ශ්‍රිතයේ නිම්නයට (තද නිල් ප්‍රදේශයට) ළගා විය හැකිය.

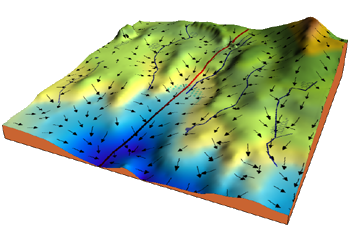රූපය 2: පිරිවැය ශ්‍රිතයක තිමාණ නිරූපනයක් එහි උපරිම බවුම් දිශාවන් (කළු පැහැ ඊ තල) සමගින්  

ශ්‍රිතය අවම වන දිශාව ඔස්සේ විචල්‍ය එනම් භාර (weights) සහ bias පදය (මෙහිදී m සහ b) පහත සම්බන්ධතාවයට අනුව නැවත නැවත යාවත්කාලීන කිරීම (update) සිදු කරයි. වැඩිම බෑවුම ඔස්සේ ගමන් කිරීම ගණිතමය ආකාරයට නිරුපනය කරන්නේ මේ අයුරිනි. මෙහිදී පෙර පියවරේ විචල්‍යයේ අගය සහ පෙර ස්ථානයේ අවකල සංගුණකය භාවිතයෙන් විචල්‍යයේ නව අගය තීරණය කරනු ලබයි. මෙහි J යනු අපගේ පිරිවැය ශ්‍රිතයයි (Cost Function). නියතය (constant), ඉගෙනුම් වේගය (learning rate) ලෙස හදුන්වයි. එය මෙම ඇල්ගොරිතමය ශ්‍රිතයේ අවම අගයට ගමන් ගන්නා වේගය තීරණය කරයි. නිවැරදි අගයන් ලබා ගැනීමට නම් මෙම අගය ප්‍රශස්ත අගයක පැවතිය යුතුය. Gradient descent ඇල්ගොරිතමය ගැන වැඩි විස්තර සදහා මෙම සබැදියට පිවිසෙන්න.

සමීකරණය 8: Gradient Descent - භාර සහ bias යාවත්කාලීන කිරිමේ සමීකරණය

පහත ප්‍රස්ථාරයෙන් මෙම විචල්‍ය යාවත්කාලින කරන ආකාරයෙන් ශ්‍රිතයේ අවමයට ලගා වන්නේ කෙසේදැයි නිරුපණය කරයි. අවකල සංගුණකය ධන වන ප්‍රදේශයේදී (දකුණු පස) විචල්‍යයේ නව අගය (w) වම් දිශාවට වෙනස් කරයි. අවකල සංගුණකය සෘණ වන ප්‍රදේශයේදී (වම් පස) විචල්‍යයේ නව අගය (w) දකුණු දිශාවට වෙනස් කරයි.

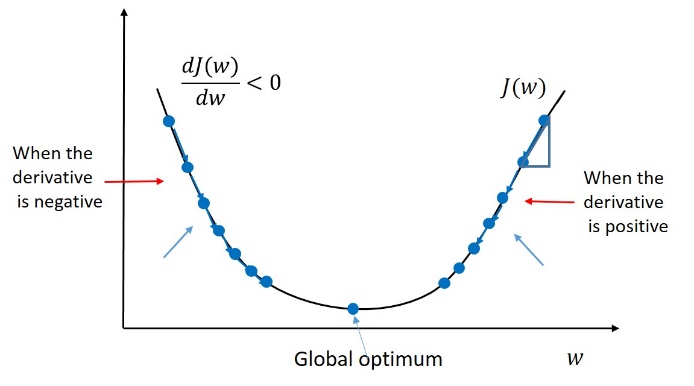රූපය 3: Gradient Descent - තනි විචල්‍යක පිරිවැය ශ්‍රිතයක අවම අගය සෙවීම

රූපය 4: Gradient Descent - විචල්‍ය දෙකක පිරිවැය ශ්‍රිතයක අවම අගය සෙවීම
source: https://miro.medium.com/max/563/0*YfUeOTUhFHtLXyrI.gif

පියවර 5: Gradient Descent භාවිතයෙන් පිරිවැය ශ්‍රිතයේ අගය අවම වන m සහ b සෙවීම

Gradient Descent ඇල්ගොරිතමය භාවිතයෙන් පහත සම්බන්ධතාවලට අනුව අපගේ විචල්‍ය දෙක නැවත නැවත යාවත්කාලින කර, පිරිවැය ශ්‍රිතයේ අගය අවම කරවන m සහ b අගයන් සොයා ගනු ලැබේ.

සමීකරණය 9:  Simple Linear Regression භාර සහ bias යාවත්කාලීන කිරිම 

අපි පිරිවැය ශ්‍රිතයේ අවම අගයක් වෙත පැමිණි බව දැන ගත හැකි එක් ක්‍රමයක් වන්නේ අපගේ පිරිවැය ශ්‍රිතයේ අගය තවදුරටත් වෙනස් නොවන තත්වයට පැමිණීමයි.

N.B: ශ්‍රිතයක අවම අගය සෙවීමට මෙවන් නැවත නැවත විචල්‍යයන් යාවත්කාලින කරමින් යන ක්‍රමයන් භාවිත කරනවා වෙනුවට සරලව ශ්‍රිතයේ උපරිම හා අවම අවකලනයෙන් සෙවීම මගින් ද සිදු කල හැකිය. නමුත් Machine Learning හිදී ස්වායක්ත විචල්‍ය දහස් ගණන් මිලියන ගණන් සහිත අවස්ථාවලදී නැවත නැවත විචල්‍යයන්ගේ අගයන් වෙනස් කරමින් යන ක්‍රමය වඩාත් කාර්යක්ෂම වේ. එම නිසා මෙම ක්‍රමය දැනගෙන සිටීම වැදගත්ය.

පහත ගැලීම් සටහන මගින් අප මෙතෙක් සාකච්චා කල ක්‍රියාවලිය සරලව කෙටියෙන් දක්වා ඇත.

රූපය 5: Linear Regression ඇල්ගොරිතමය කැටි සටහනකින්

Multi-variable Linear Regression

මෙහි ඇති එකම වෙනස නම්, ප්‍රතිදානය (Y) තීරණයකිරීමට ප්‍රදානයන් හෙවත් features (Xi) කිහිපයක්  දායක වීමයි. නමුත් අපේ සම්බන්ධතාවය තවමත් රේඛීය වේ.

සමීකරණය 10: Multiple Linear Regressionසමීකරණය 

මෙහිදී පෙර අවස්ථාවේ නොකරන ලද අමතර වූ දෙයක් සිදු කල යුතුය. එනම් ඔබ දත්ත භාවිත කිරීමට පෙර ඒවා සාමාන්‍යකරණය (normalization) කළ යුතුය. ඒ ගැන අප මීලගට සාකච්චා කරමු.

දත්ත සාමාන්‍යකරණය (Normalization)

ප්‍රදානයන් ගණන වැඩි වන විට, විවිධ ප්‍රදානයන්වල පරාසයන් ද විවිධ විය හැකිය. නිදසුනක් ලෙස, එක් ප්‍රදානයක් 0 සහ 1 අතර පරාසයක පවතින අතර, තවත් ප්‍රදානයක් 0 සහ 1000 අතර පරාසයක පැවතිය හැකිය.මෙවැනි අවස්ථාවල ප්‍රදාන හා ප්‍රතිදාන අතර සම්බන්ධතාවය සෙවීමේදී සමහර ML ඇල්ගොරිතම මෙම ප්‍රදානයන් දෙක ම එක හා සමානව තම ඉගෙනුම් ක්‍රියාවලියට දායක කර නොගැනීමට ඉඩ ඇත. මේ නිසාම සමහර විට ඇල්ගොරිතම ඉගෙනුම් ක්‍රියාවලියේදී අභිසාරී (converge) නොවීමට ද ඉඩ ඇත. අපි සියලු ප්‍රදාන එකම පරිමාණයකට හෙවත් එකම පරාසයකට ගෙන එන විට මෙම ගැටළුව තවදුරටත් නොපැමිණේ. ML ඉගෙනුම් ක්‍රියාවලියේ සුමට අභිසාරීතාවයක් සඳහා දත්ත සාමාන්‍යකරණය කිරීමේ බලපෑම පහත රූපයේ දැක්වේ. F1 සහ F2 යනු පරාසයන් විවිධ වූ ප්‍රදාන (Features) දෙකකි. 

රූපය 6: Gradient Descent අභිසරණය දත්ත සාමාන්‍යකරණය නොමැතිව සහ ඇතිව

ප්‍රදානයන් විවිධ පරාසවල පැවතීමෙන් වන තවත් ගැටළුවක් වන්නේ, සංඛ්‍යා ඉතා විශාල වන විට ගණනය කිරීම සඳහා වැඩි කාලයක් ගතවන වීමයි. විශේෂයෙන් ඉගෙනුම් ක්‍රියාවලියේදී ගණනය කිරීම් විශාල ප්‍රමාණයක් සිදු වේ. එම නිසා විශාල සංඛ්‍යා පැවතීම ඉගෙනුම් ක්‍රියාවලිය මන්දගාමී කිරීමට හේතු වේ. සියලු අගයන් පොදු කුඩා පරාසයක පවතින බව සහතික කිරීම සඳහා අපගේ ආදාන/ ප්‍රදාන  දත්ත සාමාන්‍යකරණය කිරීම කළ හැකිය. විවිධ දත්ත සාමාන්‍යකරණය කිරීමේ ක්‍රම තිබේ. ජනප්‍රිය ඒවා කිහිපයක් පහත පරිදි දැක්විය හැකිය.

Z-score Normalization:

මෙහිදී යම් ප්‍රදානයක (Xi) සියලුම දත්ත ලක්ෂ්‍යවලින් එම දත්ත සමුහයේ මධ්‍යන්‍යය/ සාමාන්‍යය අඩු කර සම්මත අපගමනයෙන් බෙදනු ලැබේ.

සමීකරණය 11: Z-score Normalization 

Min-Max normalization:

මෙහිදී යම් ප්‍රදානයක (Xi) සියලුම දත්ත ලක්ෂ්‍යවලින් එම දත්ත සමුහයේ කුඩාම අගය අඩු කර විශාලතම හා කුඩාම අගයන් අතර වෙනසින් බෙදනු ලැබේ.

සමීකරණය 12: MinMax normalization 

Logistic Normalization:

මෙහිදී යම් ප්‍රදානයක (Xi) සියලුම දත්ත ලක්ෂ්‍ය පහත සමිකරණයේ පරිදි පරිවර්තනය කරනු ලැබේ.

සමීකරණය 13: Logistic function

ඉගෙනුම් ක්‍රියාවලිය

අතරමැදි ප්‍රතිදනයන්වල දෝෂය පෙර  අවස්ථාවේ මෙන් ම ගණනය කළ හැකි නමුත් ප්‍රකාශනය පෙරට වඩා තරමක් දිගු වේ.

සම්බන්ධය 2: Multiple Linear Regression දෝෂ ප්‍රකාශනය

පිරිවැය ශ්‍රිතය හෙවත් cost function එක (මෙහිදී වර්ග මධ්‍යන්‍ය දෝෂය) පහත පරිදි තරමක් වෙනස් වේ. (මෙහිදී m යනු ප්‍රදානයක් හෙවත් features ගණන වන අතර  n යනු දත්ත සමූහයේ මුළු දත්ත ලක්ෂ්‍ය ගණන වේ)

සමීකරණය 14: Multiple Linear Regression පිරිවැය ශ්‍රිතය 

භාර පද (weights) හා bias පදයට සාපේක්ෂව පිරිවැය ශ්‍රිතයේ අවකලන සංගුනකයන් පහත පරිදි ගණනය කර ගත හැකිය. 

සමීකරණය 15: Multiple Linear Regression අවකල සංගුණක සෙවීම

න්‍යාස භාවිතයෙන් ගණනය කිරීම් සිදු කිරීම

ඔබ න්‍යාස භාවිත කරන්නේ නම්, එක් එක් භාර පදය (weight terms) සදහා ඉහත සමිකරනවල පරිදි වෙන වෙනම ගණනය කිරීම් සිදු කිරීම වෙනුවට සියලුම භාර පද සදහා ගණනය කිරීම එකවර සිදු කළ හැකිය.

10 වෙනි සමීකරණයෙන් දැක්වූ සම්බන්ධතාව න්‍යාස භාවිතයෙන් පහත පරිදි දැක්විය හැකිය. එනම් Y = XW + b යන ලෙසය .

සමීකරණය 16: Multiple Linear Regression න්‍යාස නිරූපනය 1

න්‍යාස භාවිතයෙන් අතරමැදි ප්‍රතිදානවල දෝෂය පහත පරිදි වේ.

සමීකරණය 17: Multiple Linear Regression දෝෂය න්‍යාස භාවිතයෙන්

භාර පදයන්ට (weights) සාපේක්ෂව පිරිවැය ශ්‍රිතයේ අවකලන සංගුනකයන් පහත පරිදි ගණනය කර ගත හැකිය. නමුත bias පදයට සාපේක්ෂව අවකල සංගුණකය වෙනම සෙවිය යුතු වේ. පහත සම්බන්ධතාවයෙන් අපි පෙර 15 වන සමීකරණයෙන් පෙන්වූ සම්බන්ධතාවය ම නිරූපනය වන්නේදැයි පරික්ෂා කර බලන්න.

සමීකරණය 18: Multiple Linear Regression න්‍යාස භාවිතයෙන් අවකල සංගුණක සෙවීම 

නමුත ඔබ ප්‍රදාන හා ප්‍රතිදාන අතර සම්බන්ධතාවය න්‍යාස භාවිතයෙන් පහත පරිදි නිරූපණය කරන්නේ නම් භාර පද (weights) හා bias පදයට අදාළ සියලුම ගණනය කිරීම් එකවරම සිදු කල හැකිය. මෙහිදී 16 සමිකරණයේ දැක්වූ සම්බන්ධතාවය වෙනුවට Y = XW යන සම්බන්ධය යෙදේ.

සමීකරණය 19: Multiple Linear Regression න්‍යාස නිරූපනය 2

කේතන උදාහරණ (Coding Examples)

අප මෙතෙක් සාකච්ඡා කළ සියලුම සිද්ධාන්තයන්ට අදාළ Python පරිගණක භාෂාවෙන් සිදු කලන ලද නිරූපණය කිරීම් මෙම සබැදියෙන් ලබා ගත හැකිය. ඔබට ඒවා බාගත කර ප්‍රයෝහිකව Machine Learning හි එන linear regression ඉගෙනුම් ක්‍රමය ක්‍රියාත්මක වන්නේ කෙසේදැයි යම් අදහසක් ලබා ගත හැකිය. අප විසින් මෙතෙක් සාකච්චා කරන ලද ගණිතමය සම්බන්ධතා පරිගණකයකින් නිරුපනය කරන්නේ කෙසේදැයි විමසා බලන්න.

• තවත් ලිපි සදහා පිවිසෙන්න: https://iamkasunimesha.blogspot.com/
• Python උදාහරණ : https://github.com/Kasun-Imesha/Explore-science-and-Mathematics
• simple_regression.py - Python වලින් පමණක් simple linear regression නිරුපණයක්
• simple_regression_numpy.py - simple linear regression, Python හි numpy library භාවිතයෙන් කල නිරුපනයක්. 
• multivariable_regression_matrix.py - multi-variable regression න්‍යාස භාවිතයෙන් තොර නිරුපනයක්.
• multivariable_regression_matrix_type2.py - multi-variable regression න්‍යාස භාවිතයෙන් කල නිරුපනයක්.
• multivariable_regression_matrix_numpy.py - numpy library උදව්වෙන් multi-variable regression හි න්‍යාස භාවිතයෙහි නිරුපනයක්

සටහන 

ඉහත සබැඳියේ දක්වා ඇති සියලුම කේත උදාහරණ වල (code examples) ඇත්තේ අප විසින් සාකච්චා කරන ලද සියලු ඇල්ගොරිතම මුල සිටම නිරුපණය කිරීම් ය. එම නිසා ඒවායින් සමහරක් තරමක් මන්දගාමී විය හැකිය (විශේෂයෙන් ම Numpy Library නොමැතිව කල නිරුපනයන් මන්දගාමී වේ). නමුත් ML අල්ගොරිතම් ඉතාම ප්‍රශස්ථ (Optimum) අයුරින් සාදා ඇති Libraries ඇත. Scikit-learn යනු සාම්ප්‍රදායික ML ඇල්ගොරිතම බොහෝමයක් ප්‍රශස්ත ආකාරයකින්අන්තර්ගත කර ඇති එවැනි Python Library එකකි.  එම Library භාවිතයෙන් ඔබට linear regression ගැටළුවක්  Python කේත පේළි ඉතාම සුළු ගණනකින් විසදිය හැකිය. නමුත මෙහිදී අපගේ අරමුණ වන්නේ ML හි සිද්ධාන්ත නිවැරදිව ඉගෙන ගැනීමයි. ඒ නිසා මෙම ඇල්ගොරිතම සැබවින්ම ක්‍රියාත්මකවන ආකාරය දැන සිටීම වැදගත් වේ.